monkeysber.blogg.se - Bit parity

Bit parity code#

Rather we scan only k bits where k is the total number of set bits in the number & k > 4 = 0000 1010 Based on this logic, if we compute parity, we don’t need to scan all bits. If we keep doing this, the number n will become 0 at a certain point in time. We have successfully cleared the lowest set bit (4th bit from the right side). Take an example: say n = 40, the binary representation in 8-bit format is: 00101000. In bitwise computation, if we are given a number n, we can clear the rightmost set bit with the following operation: n = n & (n-1) If we can just go over only set bits, our solution becomes little more optimized. It just goes through all bits one by one, do we really need to do that? Our concern is about set bits, so we are not getting any benefits by going over unset bits or 0 bits.

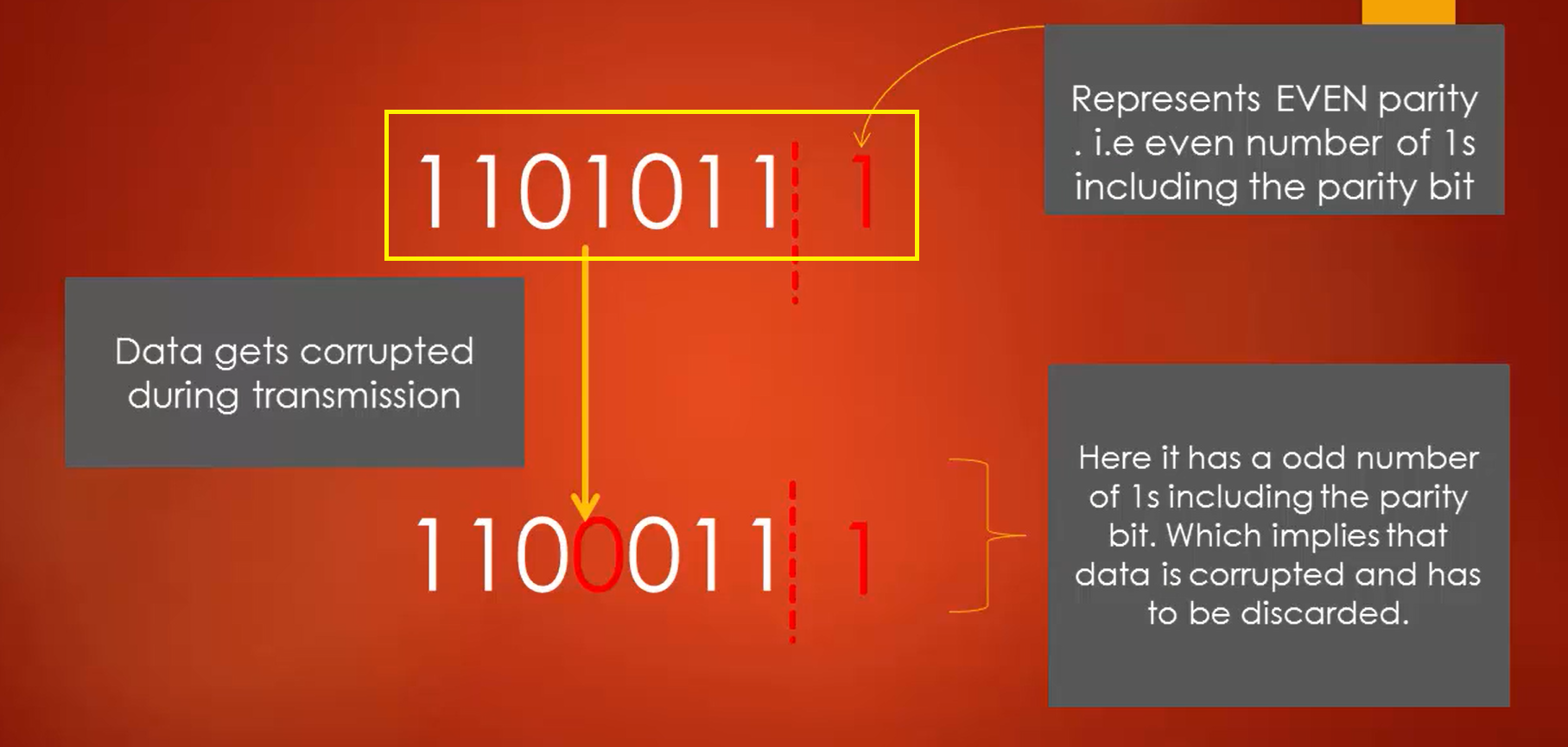
There is a bottleneck in the above solution: the while loop itself. Approach 2 - Clear all the set bits one by one: Time Complexity: O(n) where n is the total number of bits in the binary representation of the given number.

We are processing all the bits manually, so this approach is hardly efficient at scale.

The solution is very easy to understand & implement.

Finally result & 0x1 returns 1 if ther e is parity or 0 otherwise. It does not shift the sign bit in the binary representation - the sign bit remains intact at its pos ition. There is another right shift op erator - > which is called arithmetic right s hift operator.

> is logical right shift operator in java which shifts the sign bit (the most significant bit in a signed number) as well. If there are an odd number of 1’s, the final value of result will be 1. If there are an even number of set bits, eventually the result will become 0 because xor between all 1’s will cancel out each other. So when we do xor (^) operation between the current value of result & 1, the result will be set to 1 if the result is currently 0, otherwise 1. With the condition ((no & 1) = 1), we check if the current LSB is 1 or 0, if 1, we do result ^= 1.

Bit parity code#

In the above code snippet, we are going through all the bits in the while loop one by one.

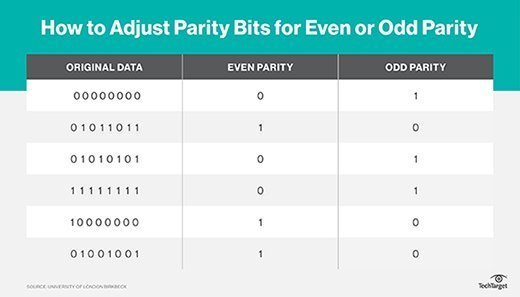
So the naive way is to keep doing a bit-wise right shift on the given number & check the current least significant bit (LSB) to keep track of the result. If the total number of set bits is odd, parity is 1 else 0. We can calculate the total number of set bits in the binary representation of the given number. The problem statement clearly states what parity is. Parity of a number is 1 if the total number of set bits in the binary representation of the number is odd else parity is 0. Design an algorithm considering such scale. Hypothetically you have to serve a huge scale like 1 million numbers per minute. You are getting a stream of numbers (say long type numbers), compute the parity of the numbers.